Image segmentation with Monte Carlo Dropout UNET and Keras¶
Given an input image, the goal of a segmentation method is to predict a segmentation mask that highlights an obect (or objects) of interest. This segmentation mask typically corresponds to a binary image of the same size as the input where pixels equal to one correspond to foreground (object) pixels and pixels equal to zero correspond to background pixels. An introductory lecture to segmentation with deep learning can be found here. The UNET is probably the most widely used architecture used for segmentation in the biological and biomedical domain. It is completely convolutional and basically corresponds to an autoencoder with concatenation (not residual) skip connections between blocks of the same spatial size. More details can be found in the original publication. Here we'll demonstrate how to build a UNET in keras and use it to perform segmentation on a publicly available biological dataset. Moreover, we'll add batch normalization between the convolutional layers and their corresponding ReLU activations. The overall architecture of the UNET used in this post is the following:
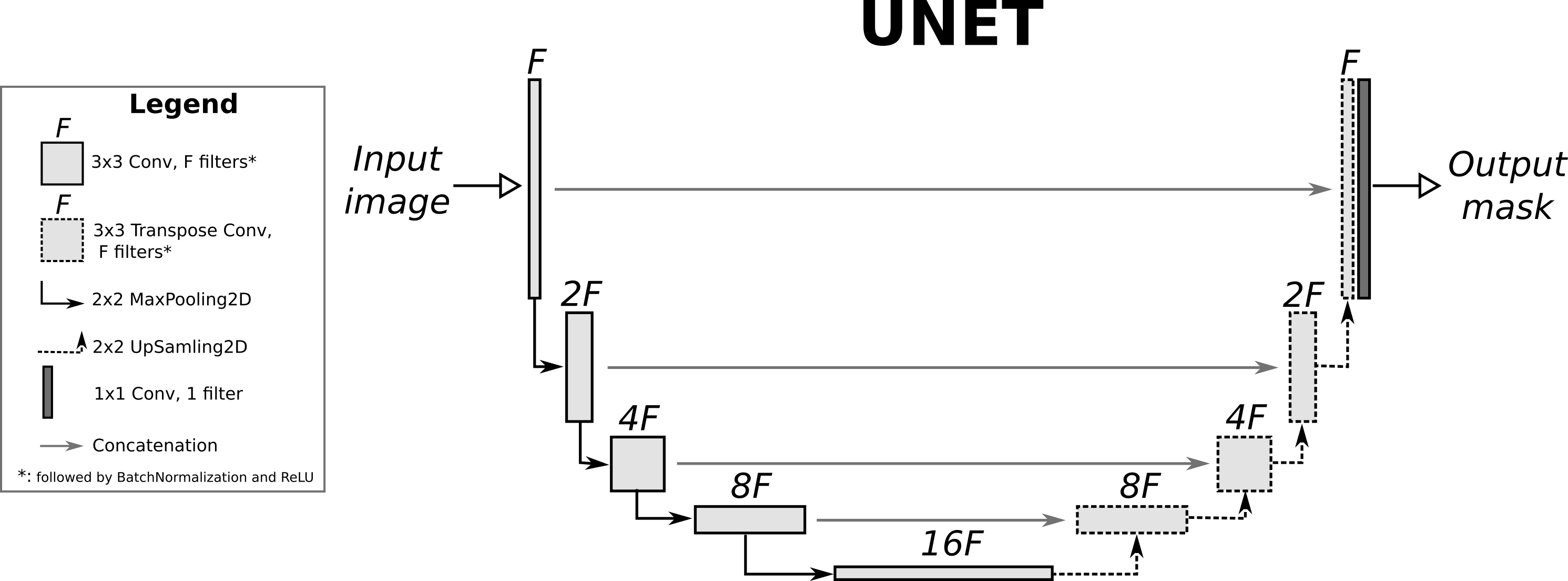
Dataset:¶
We will use the C. Elegans data available from the Broad Bioimage Benchmark Collection. The goal is to predict the segmentation mask of each image, based on the two input channels (GFP, Brightfield). Negative control worms mostly display a dead (rod-like) phenotype, while the treated worms mostly display a live (curved) phenotype. In this tutorial, we are not interested in the phenotype, just using a UNET to predict the segmentation masks. An example image of two input channels and its corresponding ground truth mask is shown below:
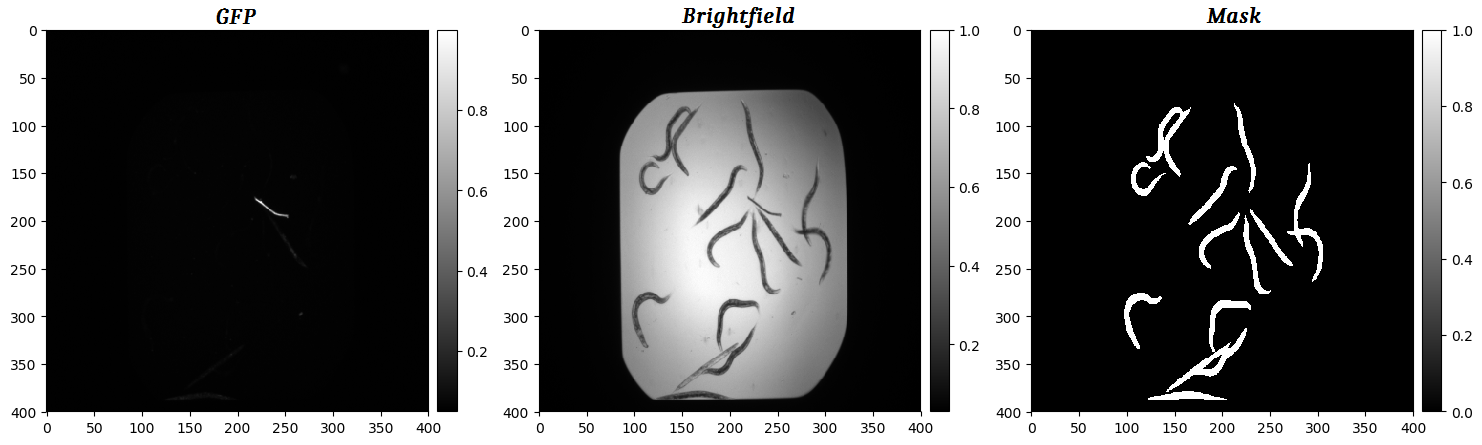 Each mask is a binary image where pixels set to one correspond to foreground (worm) and pixels set to zero correspond to background (not worm). Our goal is to train a UNET to predict the mask, based on the GFP and Brightfield channels, as shown in the concept figure below:
Each mask is a binary image where pixels set to one correspond to foreground (worm) and pixels set to zero correspond to background (not worm). Our goal is to train a UNET to predict the mask, based on the GFP and Brightfield channels, as shown in the concept figure below:
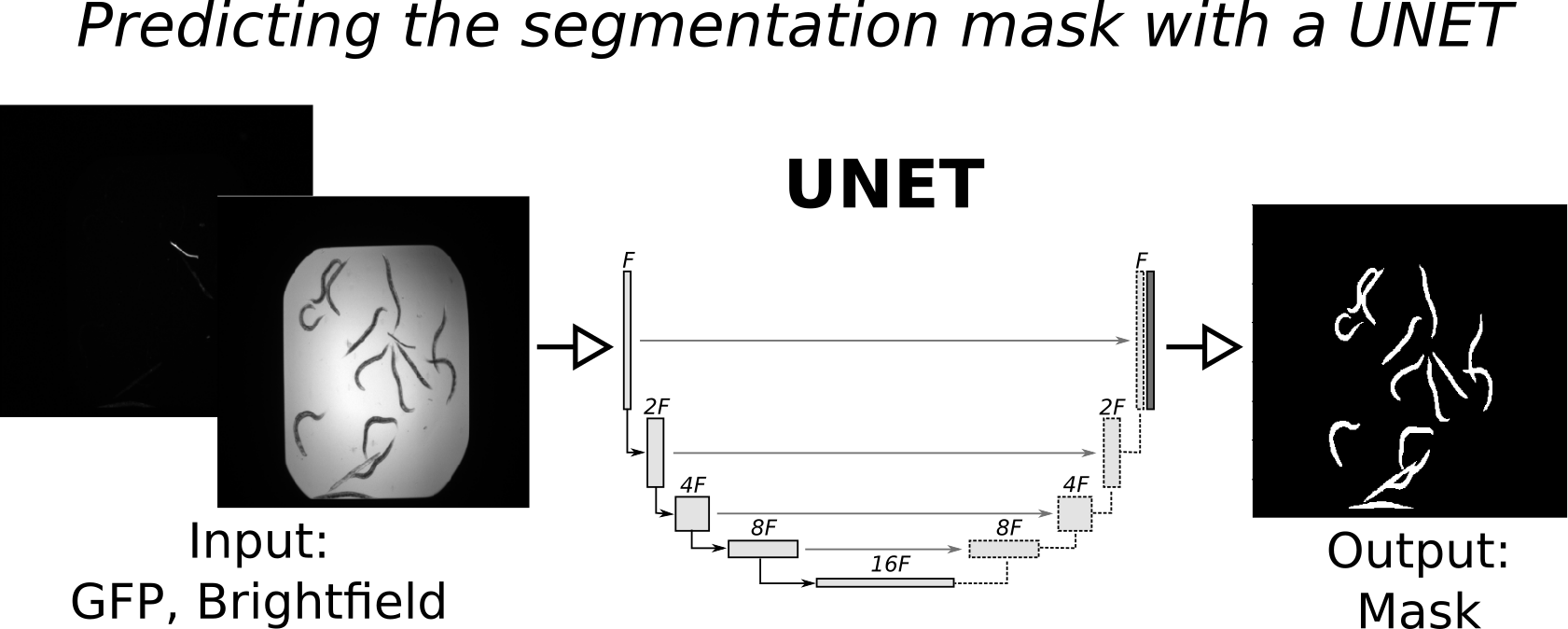
 Each mask is a binary image where pixels set to one correspond to foreground (worm) and pixels set to zero correspond to background (not worm). Our goal is to train a UNET to predict the mask, based on the GFP and Brightfield channels, as shown in the concept figure below:
Each mask is a binary image where pixels set to one correspond to foreground (worm) and pixels set to zero correspond to background (not worm). Our goal is to train a UNET to predict the mask, based on the GFP and Brightfield channels, as shown in the concept figure below:

Monte Carlo Dropout for uncertainty estimation:¶
Uncertainty estimation in the context of segmentation allows for the caclulation of uncertainty maps that depict how confident the network is about each pixel of the predicted segmentation mask. One of the most straightforward ways to modify a network to support uncertainty estimation is by using Monte Carlo Dropout. In this tutorial we will follow the process of DeVries et al. (who in turn base their approach on the bayesian SegNet). Specifically, we will add dropout layers with dropout probability of 50% in the intermediate layers of the UNET and aggregate the results of $T=20$ models (with dropout on) at inference time in order to generate the segmentation mask, as well as the uncertainty map. The architecture of the Monte Carlo Dropout (MCD) UNET is presented below:
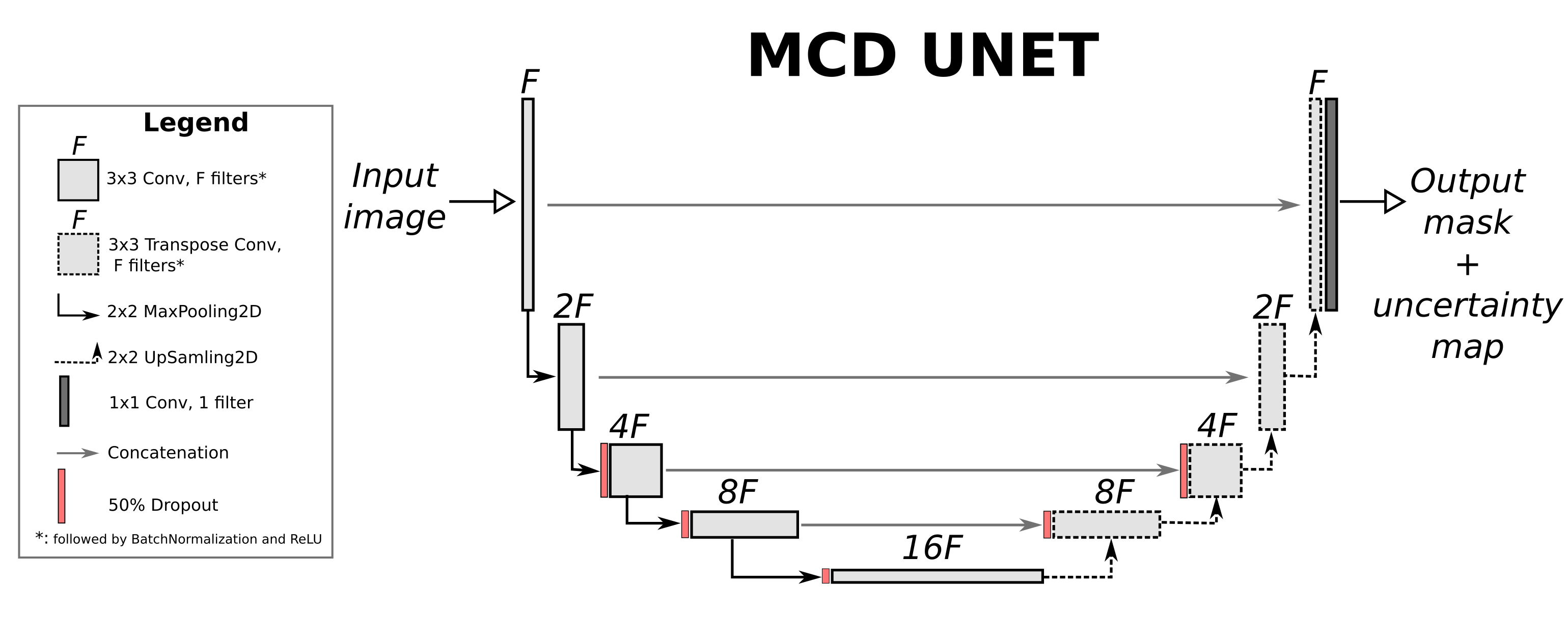 We will calculate the predicted mask as the mean mean of the 20 masks generated by the $T=20$ model instances using dropout. We will calculate the uncertainty $U$ for every pixel using the cross-entropy (check Hastie et al - page 309 for definition) over the two classes of **background** ($C=0$) and **foreground** ($C=1$) as:
$U = -(p_{C=0} \cdot ln(p_{C=0})+p_{C=1} \cdot ln(p_{C=1}))$, where $ln$ corresponds to the natural logarithm.
Another option (that we will not employ here) is to calculate the uncertainty as the variance of the $T=20$ models at each pixel (as performed in bayesian SegNet).
We will calculate the predicted mask as the mean mean of the 20 masks generated by the $T=20$ model instances using dropout. We will calculate the uncertainty $U$ for every pixel using the cross-entropy (check Hastie et al - page 309 for definition) over the two classes of **background** ($C=0$) and **foreground** ($C=1$) as:
$U = -(p_{C=0} \cdot ln(p_{C=0})+p_{C=1} \cdot ln(p_{C=1}))$, where $ln$ corresponds to the natural logarithm.
Another option (that we will not employ here) is to calculate the uncertainty as the variance of the $T=20$ models at each pixel (as performed in bayesian SegNet).
 We will calculate the predicted mask as the mean mean of the 20 masks generated by the $T=20$ model instances using dropout. We will calculate the uncertainty $U$ for every pixel using the cross-entropy (check Hastie et al - page 309 for definition) over the two classes of **background** ($C=0$) and **foreground** ($C=1$) as:
$U = -(p_{C=0} \cdot ln(p_{C=0})+p_{C=1} \cdot ln(p_{C=1}))$, where $ln$ corresponds to the natural logarithm.
Another option (that we will not employ here) is to calculate the uncertainty as the variance of the $T=20$ models at each pixel (as performed in bayesian SegNet).
We will calculate the predicted mask as the mean mean of the 20 masks generated by the $T=20$ model instances using dropout. We will calculate the uncertainty $U$ for every pixel using the cross-entropy (check Hastie et al - page 309 for definition) over the two classes of **background** ($C=0$) and **foreground** ($C=1$) as:
$U = -(p_{C=0} \cdot ln(p_{C=0})+p_{C=1} \cdot ln(p_{C=1}))$, where $ln$ corresponds to the natural logarithm.
Another option (that we will not employ here) is to calculate the uncertainty as the variance of the $T=20$ models at each pixel (as performed in bayesian SegNet).
Results:¶
We will compare the results of a standard UNET to the results of an MCD UNET of $T=20$ models. Both the UNET and the MCD UNET have the same number of 494,009 parameters, while the MCD UNET is effectively a smaller madel due to the effects of dropout. Both models are trained on the training set and a validation set is used to implement early stopping in order to prevent overfitting. The trained models are subsequently evaluated on a held out test set. Each model outputs a continuous segmantation mask $\in [0,1]$ which is subsequently binarized pixels that are either exactly zero or one, using a threshold at 0.5.
The trained UNET network achieves a median dice score of 92.4% on the left out test set, while the MCD UNET achieves a similar dice score of 90.5% while also estimating the uncertainty of the predicted segmentation maps. All test set predictions for UNET can be found here, while all test set predictions for MCD UNET can be found here. The results of the MCD unet correspond to averaged results of T=20 models with dropout probability of 50% during inference time (during model.predict()), similar to what is presented in DeVries et al., 2018.
The dice scores achieved by both models on the test set are summarized visually as follows:
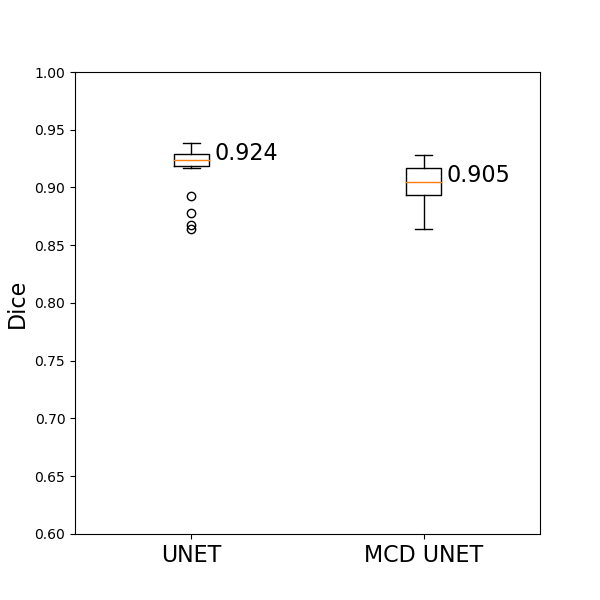 Some exemplary results for both models are the following:
Some exemplary results for both models are the following:
 Some exemplary results for both models are the following:
Some exemplary results for both models are the following:
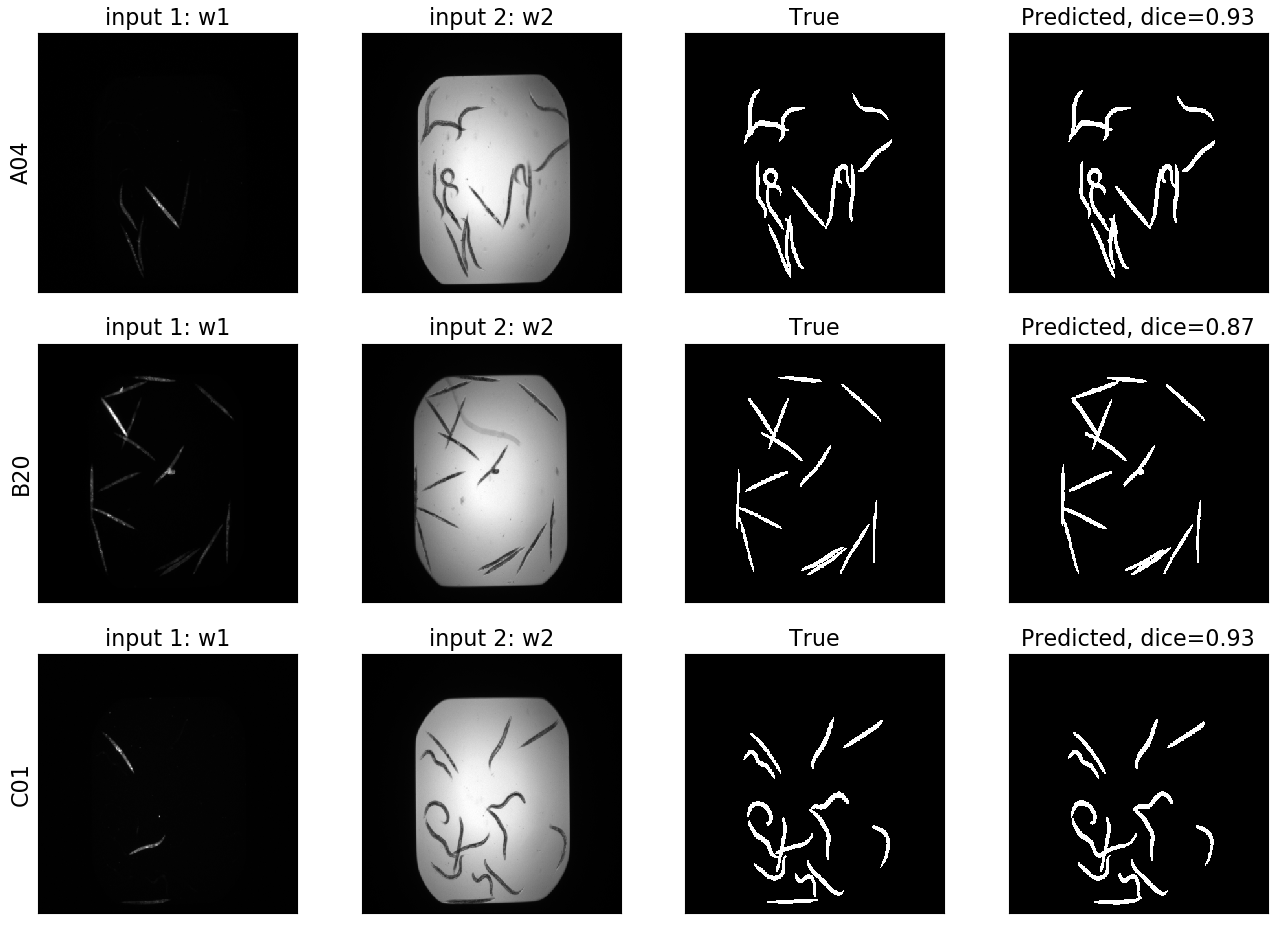
UNET¶
Here we can see the input channels, as well as the true and predicted segmentation masks.

MCD UNET¶
In the case of MCD UNET we can see the segmentation, as well as its corresponding uncertainty:


Additional Resources:¶
- paper - U-Net: Convolutional Networks for Biomedical Image Segmentation
- paper - Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning
- paper - Leveraging Uncertainty Estimates for Predicting Segmentation Quality
- paper - Bayesian SegNet: Model Uncertainty in Deep Convolutional Encoder-Decoder Architectures for Scene Understanding
- book - The Elements of Statistical Learning
Code availability¶
The source code of this project is freely available on github.